Certification d’aptitude aux fonctions de Formateur Académique

Académie de Reims session 2017-2019

Mémoire professionnel

Discipline : Mathématiques

Titre :  Comment mieux communiquer à l'écrit et à l'oral en mathématiques ? Le nouvel accompagnement personnalisé en seconde comme thème de réflexion et de progression.

Auteur : SKORNIK Karl

 

 

I.       Pourquoi avoir choisi cette problématique ?

A.     La communication : un enjeu et une compétence visés par l’ensemble des référentiels

B.     Rappel de la problématique : comment mieux communiquer à l’écrit et à l’oral en mathématiques ?

C.     Constat d’échec et ambitions :

D.     Une barrière commune : le rapport au langage

E.      Niveler l’écart entre les plus performants et les moins performants

II.     CHOIX D’UNE MÉTHODOLOGIE DE RECHERCHE

A.     Un appui théorique

B.     Des entretiens avec des professeurs

C.     Des entretiens avec des élèves

D.     Des observations en classe

E.      Un test activité préliminaire pour une individualisation postérieure : détermination du type de mémoire :

III.         DÉMARCHE DE RECHERCHE ET PROCESSUS ENGAGÉS

A.     Une première phase dédiée à la lecture et la compréhension des consignes

1.      Une première d’expérimentation :

2.      Mise en place d’un travail sur la lecture des consignes

B.     Expérimentations et remédiation sur le travail oral

1.      Une réflexion et de nombreuses interrogations

2.      Une évaluation diagnostique pour un parcours différencié

C.     Expérimentations et remédiation sur le travail écrit

1.      Développement des écrits dits « intermédiaires »

2.      Un besoin d’apports théoriques :

3.      Mise en application :

D.     Un travail de synthèse en groupe (séance d’1h30) mêlant oral et écrits de communication

IV.         PROJECTION VERS UN ACTE DE FORMATION

V.     BILAN, PERSPECTIVES ET CONCLUSION

BIBLIOGRAPHIE

ANNEXES

 

 

 

 

Comment mieux communiquer à l’écrit et à l’oral en mathématiques ? 

Le nouvel accompagnement personnalisé en seconde comme thème de réflexion et de progression.

I.               Pourquoi avoir choisi cette problématique ?

A.            La communication : un enjeu et une compétence visés par l’ensemble des référentiels en vigueur.

                         

Le choix de cette problématique résulte d’un questionnement récurrent sur les causes du décrochement observé chez de nombreux élèves en mathématiques et, en particulier, sur la frilosité affichée par ceux-ci lorsqu’il convient d’expliquer leur démarche de résolution et les choix de stratégie sous-jacents.  Les difficultés liées au passage du langage usuel au langage mathématique et réciproquement ne constituent certes pas un constat récent mais l’accent mis par les nouveaux programmes (renforcement des mathématiques dans tous les cycles) témoigne de la volonté institutionnelle de conforter les compétences des élèves dans le domaine. Il convient cependant de préciser que l’expression « langage mathématique » utilisée par les mathématiciens est à entendre comme conjugaison du langage commun avec parfois des termes exclusifs à la discipline et un symbolisme associé. Par conséquent, il n’existe pas de langage mathématique au sens premier du terme mais l’activité mathématique recourt inévitablement au langage usuel qui, associé à un symbolisme et à une appropriation (voire un détournement) de certains mots, nécessitent une compréhension du concept abordé et donc toute restitution de résultat ou de démarche. Gérard Vergnaud, didacticien des mathématiques reconnu, écrit même : « Les mathématiques ne sont pas un langage, mais une connaissance. Il est clair cependant que le langage naturel et le symbolisme jouent un rôle essentiel dans l’activité mathématique et dans l’apprentissage des mathématiques » (article Langage et pensée dans les mathématiques, revue française de pédagogie n° 96). Cette conjugaison permet alors de simplifier la manipulation et la restitution des concepts abordés. Le besoin chez l’élève d’adopter cette approche parfois complexe requiert un temps d’apprentissage certain et des efforts pour apprendre à lire et à écrire les mathématiques. L’occulter conduit aux propos parfois entendus tels que « Les maths, c’est du chinois ». G. Vergnaud évoque à ce titre la nécessité de faire cohabiter ce qu’il nomme « travail théorique utopique et travail théorique critique ».  Les évolutions récentes des programmes placent explicitement cette compétence au cœur des objectifs visés, du cycle 2 jusqu’au lycée. Cela m’a conduit à vouloir m’interroger plus intensément et précisément sur le sujet, de prendre le temps d’en explorer finement les causes et d’y trouver des pistes de réflexion et de remédiation à tester en classe et, enfin, d’élaborer une action de formation sur ce thème. À ce titre, le dispositif d’accompagnement personnalisé de la classe de seconde est précisément inscrit dans ce parcours. Il m’a donc servi de support privilégié pour expérimenter aisément et pour effectuer des orientations pédagogiques et didactiques adéquates aux côtés d’élèves peu à l’aise dans la discipline, également pleinement intégrées dans mes pratiques quotidiennes hors accompagnement personnalisé. 

B.            Rappel de la problématique : comment mieux communiquer à l’écrit et à l’oral en mathématiques ? 

Le nouvel accompagnement personnalisé en seconde servira de support comme thème de réflexion (à posteriori d’évaluations diagnostiques qui y seront menées) et comme axe de progression, l’effectif réduit implicite à ce dispositif facilitant les échanges et donc l’analyse. Toutefois, la plupart des orientations didactiques et pédagogiques émergentes ont également trouvé leur place en classe entière car aisément transposables. Cela m’a alors permis de dégager les spécificités propres au dispositif choisi et d’obtenir une vision plus globale. 

C.            Constat d’échec et ambitions : 

 

Voici (via le flashcode ci-contre ou le lien associé de la sitographie) un extrait d’un reportage diffusé sur BFMTV qui, malheureusement, reflète ce que l’on entend fréquemment auprès de nos élèves ou de leurs parents. Il symbolise ladite fracture perçue entre les mathématiques et les élèves qui s’y trouvent en difficultés, en outre  matière souvent qualifiée de « bête noire » par ceux-ci. Dans les classes, selon les enseignants, c’est en résolution de problème que le décrochage touche le plus d’élèves, puisqu’il convient alors d’engager des compétences et non plus simplement des connaissances. Vous trouverez en annexes 1 à 3 le bilan d’études internationales, une analyse de celle-ci et différents points de vue convergents (élève, professeurs, institution) quant au constat inquiétant et lattant dressé par l’ensemble des acteurs de la communauté éducative sur le sujet. J’en partage le bilan à travers mes observations quotidiennes en classe. Je me refuse à tout défaitisme infructueux et vraisemblablement exagéré mais je parlerai plutôt de frilosité observée face à la discipline. Force est de constater celle-ci, par exemple, à travers la rareté de la présence des mathématiques, tant à l’écrit ou à l’oral, dans l’épreuve anticipée de TPE (Travaux Personnels Encadrés) notamment en série S, pour lesquels le choix des deux disciplines supports du projet incombe aux élèves et, malheureusement, se porte rarement sur les mathématiques. La justification d’une majorité d’élèves peut se résumer en « il est difficile de parler de maths » alors que le rôle fondamental de

la discipline dans la banque de thèmes suggérés émerge aisément. Les difficultés apparaissent également nombreuses lors de la passation des CCF de BTS, où l’oral et l’écrit se conjuguent. Par conséquent, réfléchir aux causes de cette appréhension et en amorcer des pistes de remédiation et/ou d’anticipation me semble naturel, sentiment conforté par la réforme du « baccalauréat 2021 » projetant une épreuve qualifiée de « grand oral ».  

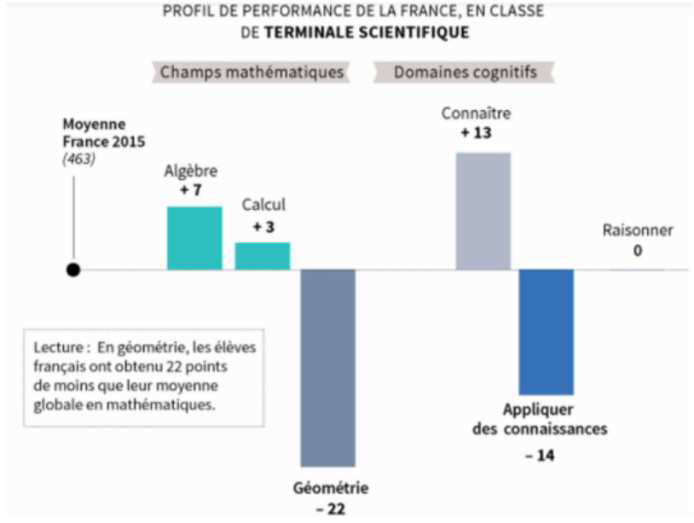
Difficultés à réinvestir les connaissances (extrait annexe 1, Le Monde 29 novembre 2016)

 

D.            Une barrière commune : le rapport au langage 

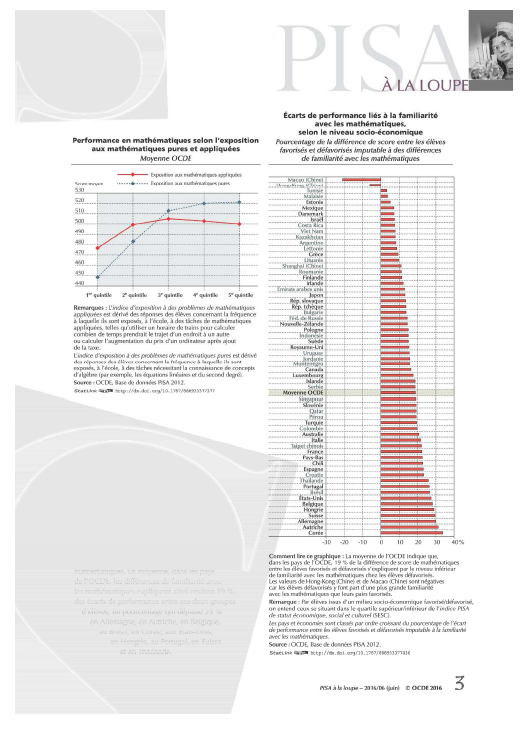
Il ne convient pas de stigmatiser les pratiques des enseignants de mathématiques ou les programmes ou encore le système de formation comme il l’est dit dans le reportage mais de tenter modestement de percevoir et de dégager des solutions via un biais reconnu comme source de difficultés récurrentes, à savoir la communication en mathématiques. D’autres facteurs influents (sociaux par exemple) ne seront pas abordés explicitement mais ont été sources de lecture et réflexion afin d’enrichir mes connaissances et de globaliser ma vision du sujet (annexe 3, étude Pisa). 

                                             

 

La question du langage en classe des mathématiques est usuellement abordé selon trois points de vue :

• Son rôle comme objet d’étude

Un énoncé de mathématiques est souvent codifié par une expression symbolique et/ou des mots rencontrés dans un contexte presque exclusivement disciplinaire. De plus, le message est tel un algorithme dont l’interprétation est univoque. Les énoncés des exercices, souvent courts, semblent dénués de difficultés aux yeux de l’enseignant se limitant le plus souvent à des énoncés courts de l’ordre de deux à trois phrases. Quant à l’autre source fréquente d’activités, à savoir les problèmes, leur énoncé tend à être développé et fortement contextualisé. Quant aux textes explicatifs, aux textes de démonstrations ou encore aux exercices résolus, ceux-ci engendrent implicitement des traces écrites plus longues. Ces différents types de textes, par leur longueur et en raison de l’enchaînement d’informations parfois peu hiérarchisées ou peu explicites, requiert une attention particulièrement soutenue et une capacité de stockage mémorielle adéquate. Par conséquent, il est légitime de penser que les élèves souffrant de difficultés de mémorisation n’en conservent qu’une représentation partielle des informations à traiter. Ce manque conduit à une mauvaise compréhension du texte mathématique et par conséquent, à une mauvaise transcription orale ou écrite. À cet effet, un test de détermination du type de mémoire individuelle a été proposé auprès d’un échantillon d’élèves (annexe 4).

• Son rôle dans les apprentissages

Le langage, oral ou écrit, joue un rôle central dans les activités des élèves et en particulier dans leur articulation avec celle de l’enseignant. Découvrir, s’approprier et maîtriser de nouveaux concepts requiert nécessairement une association entre ceux-ci et les pratiques langagières, ces allers-retours permanents s’alimentant mutuellement. À cet effet, une réflexion sera menée quant à la progressivité à adopter pour garantir une compréhension évolutive et satisfaisante du vocabulaire et des représentations lors de l’approche d’un nouveau concept : quel(s) mot(s) choisir pour nommer un concept abstrait ? Comment exprimer une idée pour que le vocabulaire employé n'en ralentisse pas l’assimilation et réciproquement ? Quel travail oral effectuer pour y parvenir ? Quel travail écrit ? Une attention particulière sera portée sur le rôle et l’impact des écrits dits « intermédiaires ».  

• Le langage comme outil pour enseigner

Les mathématiques s’enseignent et s’évaluent en français, leur enseignement participe à l’apprentissage de la langue et à son utilisation dans l’expression, la formulation d’une pensée ou la réflexion sur une signification. Par leur recours à des registres multiples (formel, graphique, tableau, algorithme, …) avec lesquels il convient de savoir jongler, un apprentissage des règles du langage mathématique est également nécessaire. Moyen d’apprentissage (rôle précisé ci-dessus), le langage constitue dès lors un levier d’enseignement. Les mots prononcés, les expressions, les formulations de l’élève témoignent de son activité en classe, de son apprentissage et de son degré d’acquisition des concepts engagés. En outre, le langage représente un outil que le professeur  peut guider et piloter à travers les actions que sont : faire formuler, faire reformuler , faire échanger entre eux. Celles-ci mènent implicitement à faire penser l’élève, à le faire penser autrement et, de fait, à faire évoluer ses conceptions. Sylvie Cèbe dit à cet égard : « On les (les élèves) laisse tâtonner, explorer, découvrir les meilleures manières de faire, sans, parfois, leur expliquer comment on fait pour bien faire » (cf. vidéo citée dans la sitographie). Par conséquent, le langage utilisé par le professeur lui-même constitue un outil primordial et très influent, tant à l’oral qu’à l’écrit mais la latitude offerte requiert de manipuler des expressions cohérentes et explicites, des formulations variées, en garantissant les équivalences des expressions utilisées. Il convient également de veiller à adapter le langage à l’instant et aux circonstances de l’apprentissage.  

           

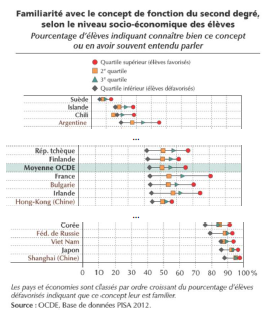
E.             Niveler l’écart entre les plus performants et les moins performants

Ce mémoire n’aura pas pour intention de lister et de commenter les causes et origines de ces écarts, nombre de recherches ayant été effectuées sur le sujet. Je me suis, à mon niveau, modestement restreint à prendre connaissance de quelques-unes d’entre elles par la lecture d’articles (annexes 1,3 et Denis Butlen dans Grand N 79 IREM de Grenoble, 2007) et à construire des parcours différenciés pour l’accompagnement personnalisé de seconde. Toutefois, ma progression s’est effectuée en gardant à l’esprit la corrélation entre la dimension des difficultés rencontrées en mathématiques et le niveau social des élèves. Comme le relate l’OCDE en juin 2016 (PISA à la loupe, n°63), « les élèves défavorisés sont moins familiers avec les concepts mathématiques », or « l’exposition aux concepts et procédures mathématiques a une incidence sur la performance » et « la familiarité avec les mathématiques est liée à l’écart de performance entre les élèves favorisés et leurs pairs défavorisés ». Cela m’a donc conduit à axer mes recherches sur les leviers qui me sont accessibles, à savoir la familiarisation avec la pratique langagière mathématiques (il n’existe pas un langage mathématique mais une appropriation du langage usuel) à travers des activités visant à donner confiance à l’élève, facteur corrélé à la performance mathématique, comme le précise et le détaille Elisabeth Bautier (Lire et écrire pour apprendre, conférence université de Liège, mars 2017). Un intérêt particulier sera porté sur la phase des écrits intermédiaires qui me semblent être trop souvent occultés dans les apprentissages en tenant compte du travail effectué à ce sujet par Jean-Charles Chabanne et Dominique Bucheton (Parler et Écrire pour penser, apprendre et se construire, PUF 2002) : « intermédiaire peut être pris dans de nombreux sens : intermédiaire entre deux états d’un écrit à mettre en forme, entre deux états de pensée, entre les membres d’un groupe de travail, entre des écrits et des oraux, etc ». Il est alors « une médiation entre deux sujets, entre deux discours, entre le sujet et lui-même » et possède un « caractère transitoire et lié à des situations précises de travail ». L’importance de cette phase sera confirmée par les conclusions résultantes des entretiens avec les élèves (voir bilan de ceux-ci). 

II.                  CHOIX D’UNE MÉTHODOLOGIE DE RECHERCHE

A.            Un appui théorique

« Il n’y a pas de raison à l’échec en mathématiques : il n’y a que des raisons » écrivait Stella

Baruk en phrase d’introduction de son ouvrage Echec et Maths, Editions Seuil 1973. Afin d’étoffer mes connaissances extra disciplinaires pour cerner lesdites raisons, un temps préparatoire a donc été consacré à diverses lectures. Un rapport de l’inspection générale de mathématiques (Les traces écrites des élèves en mathématiques, 2001) m’a fourni une évaluation diagnostique précise et approfondie, portant sur un échantillon d’élèves que je n’aurais pu obtenir. Certes, celui-ci a été rédigé depuis presque vingt ans mais demeure d’actualité, les constats affichés pouvant être encore fréquemment lus, observés ou entendus. Cette lecture m’a inspiré pour élaborer mes supports et activités de remédiation présentés plus loin dans ce mémoire. Toutefois, j’ai tenu à réaliser également les entretiens avec certains collègues et mes élèves de seconde (selon les trames proposées dans le rapport et figurant en annexes 5 et 6) pour certes y retrouver des réponses très voisines du bilan figurant dans le rapport mais cela m’a permis des échanges visant à sensibiliser ceux-ci à ma démarche et à leur préciser le sens des tests et du parcours différencié à venir.  

Pour un accès direct au rapport complet :   

B.            Des entretiens avec des professeurs

L’objectif de ces entretiens étaient de cerner plus précisément le type de traces écrites produites puis le lien entre celles-ci et l’activité mathématique des élèves au sein d’une classe. Les échanges ont été mené de vive voix, la trame me servant de support n’ayant volontairement pas été distribuée aux collègues afin de pouvoir percevoir clairement leurs priorités (hiérarchie et temporalité du discours). La place de l’oral a également été abordée : quand et sous quelles formes ? Tous pointent du doigt les difficultés de lecture et de construction du sens que les élèves rencontrent en résolution de problème. Ils établissent un rapport direct avec la compréhension de la langue écrite. Je distinguerai toutefois les réponses obtenues auprès de collègues enseignant en collège et ceux exerçant en lycée. Il apparaît clairement que ces derniers considèrent majoritairement les difficultés langagières moindres et imputent davantage les lacunes des élèves à des lacunes techniques essentiellement liées au calcul. Le contenu observé des séances d’accompagnement personnalisée témoigne de ce sentiment, elles s’apparentent davantage à du soutien disciplinaire visant à ancrer les procédures de résolution des exercices ou des problèmes sous-jacents aux notions abordées sur le moment. Il ressort également que plus les élèves sont perçus comme en difficultés, plus leur sont proposés des pratiques « rigides » laissant peu d’initiative et d’autonomie chez les apprenants : « il faut apprendre le cours et reproduire mot pour mot les méthodes », ancrant ainsi les traces écrites dans des modèles stéréotypés. En outre, la référence à l’examen terminal (à savoir le baccalauréat) est récurrente et constitue une source de pression et d’orientation didactique marquée : « il faut préparer les élèves et renforcer le bagage technique » m’a confié un collègue. Ce poids incite indéniablement à orienter ces derniers vers un apprentissage répétitif visant à apprendre prioritairement des méthodes de résolution, rassurantes mais privant d’une compréhension satisfaisante des concepts mathématiques associés. Or, l’évolution des sujets de baccalauréat dans les disciplines scientifiques tendent à proposer des exercices à prise d’initiative pour lesquels la méthode de résolution n’est pas explicite mais demande en amont une modélisation, ou une appropriation à minima de la situation et d’en dégager ensuite les connaissances sous-jacentes. Cette stratégie pédagogique n’invite que trop peu l’élève à élaborer un raisonnement personnel et donc à s’exprimer. 

C.            Des entretiens avec des élèves

Les entretiens ont été individuels sur une durée moyenne de 20 minutes environ. Tout d’abord, cette démarche a surpris les élèves, particulièrement par la présence de questions d’ordre général sur leur perception des mathématiques placées au début de l’entretien, visant à « sortir » l’élève de sa représentation habituelle de la matière comme unique discipline scolaire. Beaucoup de questions restaient sans réponse si je ne prenais pas l’initiative de leur faire analyser leurs propres pratiques, lesquelles étaient ignorées ou n’avaient jamais été l’objet d’une autoanalyse (cf. de nouveau Sylvie Cèbe citée p6).  

D.            Des observations en classe

Effectuées sur 5 classes de seconde, explicitées et analysées ultérieurement dans ce mémoire.

E.             Un test activité préliminaire pour une individualisation postérieure : détermination du type de mémoire :

Afin d’élaborer mes expérimentations, il m’est apparu nécessaire de m’intéresser tout d’abord au mode de fonctionnement de la mémoire à travers les différents supports qui peuvent être utilisés en classe. Cette interrogation et ce constat de manque de connaissances de ma part sur le sujet m’interpellaient d’autant plus que la multiplication des supports multimédias depuis quelques années nous amène à effectuer des choix didactiques. Mais, alors, avec quelle influence respective sur les apprentissages ?   Je retiendrai de mes lectures à cet effet cette synthèse (article d’Alain Lieury, portail CAIRN.info sur le n°130 de la revue Etudes de Linguistique Appliquée, 2003)

 

 

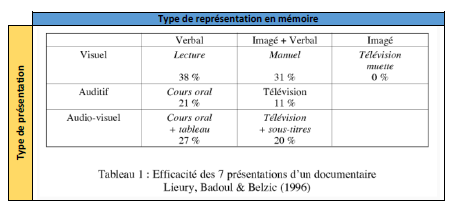
En outre, ces lectures m’ont permis d’éluder certaines représentations partiellement erronées que j’avais et m’ont permis d’orienter les types de support que j’allais construire comme outils de remédiation destinés à aider les élèves à mieux communiquer en mathématiques. Je n’en dresserai pas une liste exhaustive mais retiendrai la conversion quasi-systématique de toute représentation en une verbalisation vers la mémoire lexicale (passage des mémoires sensorielles à la mémoire sémantique). La faible taille de l’échantillon des élèves ayant répondu au test de détermination du type de mémoire (ou plus précisément au repérage des types de présentation privilégiés) ne me permet pas d’en tirer des conclusions formelles mais de constater cependant que les quelques élèves dits de type kinesthésique (qui exploitent moins les présentations visuelles et auditives) sont en échec pour la plupart en mathématiques et que ceux exploitant représentation visuelle et auditive pour la construction de leur mémoire semblent les plus à l’aise. Je ne tire aucune conclusion (même si cela est tentant) qui n’aurait aucune valeur scientifique étant donnée la très faible taille de l’échantillon. 

• Objectifs et mode de passation

La première séance d’accompagnement personnalisée a donné lieu à un test de détermination du type de mémoire de chacun des élèves, afin de leur donner un nouveau repère à considérer dans leurs pratiques. Il me permettra également de différencier les parcours d’activités proposés. Cette action a tout d’abord surpris la classe. Le bilan prospectif a été effectué avec les élèves en proposant des aides (annexe 4).

• Bilan et perspectives

Menée dans ma classe, elle m’a permis de confirmer mon hypothèse de départ, à savoir pour la première phase, la faible proportion du travail écrit autre que la reprise du cours et, pour la seconde, la prédominance des mémoires orale et écrite. Afin d’essayer de pallier les obstacles liés à la langue écrite, j’ai décidé de mener des entretiens avec les élèves, plus approfondis, visant à faire expliciter les représentations et les organisations de l’élève, toujours selon une trame inspirée par le rapport de l’Inspection Générale de Mathématiques déjà évoqué en 2.a).

III.            DÉMARCHE DE RECHERCHE ET PROCESSUS ENGAGÉS

 

              Préambule      

• Les différents types d’écrits sollicités en mathématiques : détection de « maillons faibles »

Pourquoi faire cette distinction ? Les observations de classes en mathématiques nous montrent l'existence d'un certain nombre d'éléments : des écrits de référence (cours, correction des exercices majoritairement), des brouillons, des récits, des schémas, des figures, des brouillons ou des écrits « intermédiaires » qui sont, pour ces deux dernières catégories, partie prenante de l'activité mathématique mais qui sont insuffisamment (ou pas du tout) valorisés par l'institution. Celle-ci valorise essentiellement les écrits qui correspondent à des pratiques d'évaluation ou de tenue de cahiers contrôlés par l’enseignant, ce qui permet de rendre visible le travail et peut être contrôlé socialement, notamment par les parents.

• Le rôle et la dimension de l’oral en mathématiques :

Nul ne peut ignorer la nécessité d’une pratique de l'oral pour construire les savoirs et accéder aux processus d'apprentissage des élèves. Je me souviens de certains visages de mes élèves de seconde lors de l’énoncé de la propriété :

Il me semble alors intéressant de se poser la question de ce que comprend un élève lorsqu’il entend en classe ce type d’énoncé. Le besoin de développer pour ceux-ci un répertoire langagier plus riche d’une part, et d’autre part de trouver des aides-passerelles entre son langage propre, le langage de la salle de classe, le langage académique du manuel. Différents types de langage cohabitent dans la classe : langage entre élèves (échanges entre pairs), langage dans les échanges professeur/élève(s), langage lorsque le professeur expose, langage académique des manuels, langage scientifique (revues scientifiques ou de vulgarisation par exemple). Le professeur joue le rôle de médiateur entre les différents discours. Il lui revient de prendre conscience du langage qu’il utilise afin d’obtenir une analyse réflexive de sa pratique. Le travail de l’élève à l’oral est indispensable pour accéder à la compréhension, alors nous verrons en quoi il est aussi du ressort du professeur de mathématiques.

• Diagnostiques et mise en place d’un parcours différencié de remédiation, interactions, projection :

Suite aux entretiens, j’ai choisi de procéder selon le déroulement suivant :

                             . Phase dédiée à la lecture et la compréhension des consignes ;

                             . Expérimentations et remédiation sur le travail oral ;

                             . Expérimentations et remédiation sur le travail écrit ;

                             . Travail de synthèse mêlant oral et écrits de communications.

 

A.                  Une première phase dédiée à la lecture et la compréhension des consignes

1.                         Une première d’expérimentation :

Une observation récurrente concerne la difficulté éprouvée par les élèves à distinguer la tâche implicite aux verbes utilisés dans les énoncés (méconnaissance du mot, du sens de celui-ci ou encore nuance par rapport à un autre). J’ai tout d’abord listé les verbes figurant dans le sujet de mathématiques du DNB 2018 (sujet Métropole), qui étaient : donner, expliquer, déterminer, calculer, justifier, représenter, compléter, exécuter. Le test (annexe 5) proposé en accompagnement personnalisé sur la lecture de consignes a été mené conjointement avec la professeure de français en charge de la classe avec pour objectif d’offrir une approche générale de la compétence visée ainsi qu’une approche disciplinaire comme proposé dans l’exercice 2 :

                    

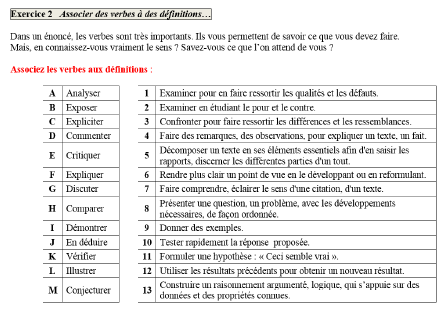
La séance fut poursuivie et complétée par un exercice consistant à formuler une (des) question(s) pouvant être associée(s) à des solutions d’exercices divers. 

2.             Mise en place d’un travail sur la lecture des consignes

La spécificité du vocabulaire et de la syntaxe utilisés en mathématiques nécessite un travail spécifique relatif à la lecture des textes propres à la discipline. En effet, ces textes diffèrent de ceux rencontrés usuellement dans d’autres disciplines (français, langues vivantes, histoire-géographie, …) et leurs particularités doivent être prises en compte dans les apprentissages. On ne lit pas de la même façon la consigne d’un exercice, la description d’une figure ou d’un schéma, le texte d’un problème, le cours, le manuel ou encore les graphiques. Le bilan de l’activité précédente a mis en avant des difficultés quant à l’explicitation des consignes. Une attention particulière à cet égard a donc été portée sur la diversité des supports utilisés dans le questionnaire flash d’évaluation diagnostique ci-dessous (forme des supports, alternance cadres graphique et algébrique, alternance vocabulaire usuel et mathématique, …). 

B.                    Expérimentations et remédiation sur le travail oral

 

1.             Une réflexion et de nombreuses interrogations

 

Trois séances d’accompagnement personnalisé furent consacrées à un travail sur l’oral avec pour objectif d’inciter les élèves à inclure cet aspect dans leur(s) mode(s) d’apprentissage. Il m’est donc apparu nécessaire de m’interroger sur les situations qu’il convenait de proposer et d’envisager des outils d’évaluation pour en mesurer la perspicacité. Or les difficultés éprouvées et le temps d’analyse consacré témoignent certainement d’un manque de réflexion et de pratique sur le sujet. Former les élèves à s’exprimer à l’oral n’est donc pas si simple qu’il n’y paraît pour l’enseignant, cela constitue un apprentissage de l’élève mais également du professeur dans ses pratiques.  

Par conséquent, il convenait alors d’envisager cette formation à l’oral de mes élèves par un travail sur les situations d’oral entre enseignants de matières différentes, chose faite lors de la seconde heure d’accompagnement personnalisé consacrée à l’oralité (dispositif propre à l’établissement avec deux projets semestriels pour chaque élève). Pour l’autre heure, consacrée aux mathématiques, il m’a tout d’abord fallu me questionner sur mes représentations sur ce qu’est :

• Travailler pour un élève ?
• Apprendre pour un élève ?
• « Un élève qui travaille » pour le professeur ?
• Prendre la parole pour un élève ?
• Ecouter pour un élève ?

Il convenait également de se demander à quelles occasions les élèves prennent la parole en classe dans le cadre du cours de mathématiques. A cet égard, j’ai finalement décidé de poser ces questions à mes collègues enseignants de mathématiques et à mon groupe d’élèves d’accompagnement personnalisé pour enrichir et étayer ma réflexion personnelle.

• Questions posées aux enseignants :

À quelles occasions les élèves prennent-ils la parole : 

• pour demander s’ils n’ont pas compris ?
• pour répondre à une question du professeur ?
• pour montrer qu’ils participent au cours ?
• pour donner un avis ? pour débattre ?
• pour contester un avis, une proposition ?
• pour présenter un exercice, une recherche personnelle ?
• pour défendre un point de vue ?
• pour rapporter des propositions d’un sous-groupe ?
• pour commenter une réponse ?
• pour lire un texte ?
• pour reformuler pour quelqu’un ?

• Questions posées aux élèves :

Avez-vous le sentiment de participer oralement en classe ?

Si oui :

                                                                     Volontairement ? Si vous êtes interrogé ?

                                                                 A quels moments ? Pour quelles raisons ?

                                                      Si non :

                                                                  Pour quelles raisons ?

Pour les élèves, ce questionnaire fut déroutant car il les interrogeait sur des questions qu’ils n’ont pas pour habitude de se poser ou d’entendre. La participation orale se cantonne à « répondre à une question si je suis interrogé » ou « poser une question si je n’ai pas compris ». Cependant, ces questions leur ont permis d’entrevoir d’autres moments et d’autres façons de développer leur participation.   

Tant pour les élèves que pour les professeurs, la digression de la participation à l’écoute est très forte, voire de plus en plus forte. Pour les enseignants, les raisons invoquées sont étroitement liées à la gestion de classe notamment en seconde. Pour les niveaux supérieurs, « on n’a pas trop le temps de s’attarder » confient la plupart des collègues. Le besoin de quantifier rapidement la plus-value d’une pratique est palpable. 

Pour les élèves, il faut « écouter le professeur pour suivre et comprendre ». Pour les collègues, il faut aussi « écouter le professeur, ses camarades, pour prendre en compte, pour donner et confronter des points de vue, en respectant des règles d’intervention ». 

Il convenait alors de dégager, dans un premier temps, des situations favorisant une réelle participation orale, constructive et favorisant les apprentissages puis, dans un second temps, les activités associées. Ces questions renvoient à notre remarque préalable relative à l’importance des situations que les élèves vivent en classe. Ce sont les dispositifs, les situations, les démarches mises en œuvre dans la classe pour que les élèves apprennent qui donnent du sens à une volonté collective des enseignants de développer des compétences d’oral. Le travail d’une équipe d’enseignants sur l’oral, si on ne dépasse pas la conception « oral-participation » est sans issue. La mise en place d’une situation puis d’une tâche discursives, au sens où les décrivent Claudine Garcia-Debanc et Isabelle Delcambre

(Repères, recherches en didactique du français langue maternelle, n°24, 2001) permet « de comprendre où se situe l’activité de l’élève dans la situation conçue par l’enseignant ».

Outre la mise en place de différentes situations favorables, il convient également d’en préciser les critères de réussite (travail effectué lors des ateliers mis en place sur le créneau d’accompagnement personnalisé transversal sur l’oralité), de placer les élèves en situation de confiance (valoriser la participation). 

Selon Alfred Bertolucci (L’oral en mathématiques dans PRATIQUES Math, bulletin n°45 des groupes de recherche Math-collège, Math-lycée et Primaire du CEPEC, 2011), il convient de considérer quatre familles de situations de formation à l’oral en mathématiques :

• Rendre compte à l’oral d’une réalisation, d’une recherche de l’élève ;
• Reformuler oralement des informations lues (texte court, énoncé par exemple) ; ● Prendre part de façon organisée à une discussion collective dans la classe ; ● Évaluer la prise de parole dans ou devant un groupe.

Afin de préparer les expérimentations, plusieurs lectures furent consacrées aux entretiens d’explicitation. Outre les vidéos et articles de Sylvie Cèbe déjà cités, des apports théoriques ont été obtenus dans une brochure de l’IREM de Lyon (L'entretien d'explicitation en situation scolaire, 2003) et de l’ouvrage de Pierre Vermersch et Maryse Maurel (Pratiques de l’entretien d’explicitation, 1997). Fort de ces préconisations et lectures, voici ci-dessous les expérimentations effectuées.

2.             Une évaluation diagnostique pour un parcours différencié

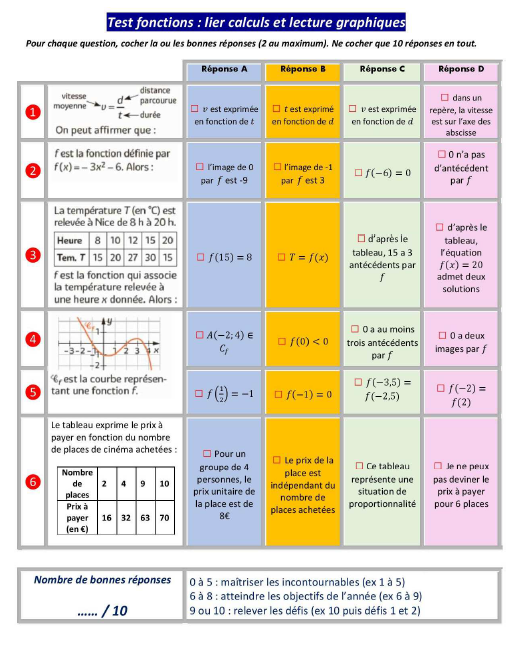
Le travail d’explicitation et les échanges oraux trouvent toute leur place en mathématiques pour faciliter la compréhension de la situation proposée, de l’énoncé en amont de l’engagement de l’élève dans son activité mathématique. Les écrits ne peuvent représenter le seul mode de communication des actions en mathématiques. Les éventuelles difficultés liées au vocabulaire (usuel ou spécifique à la discipline) ou/et à la lecture ne doivent pas entraver, voire rendre impossible la progression des élèves et l’exploitation des compétences déjà acquises. À cet effet, une première activité de remédiation fut proposée à la classe : un questionnaire (activité flash annexe 8) d’évaluation diagnostique sur les fonctions visant à obtenir les compétences de chacun en amont du traitement du chapitre. 

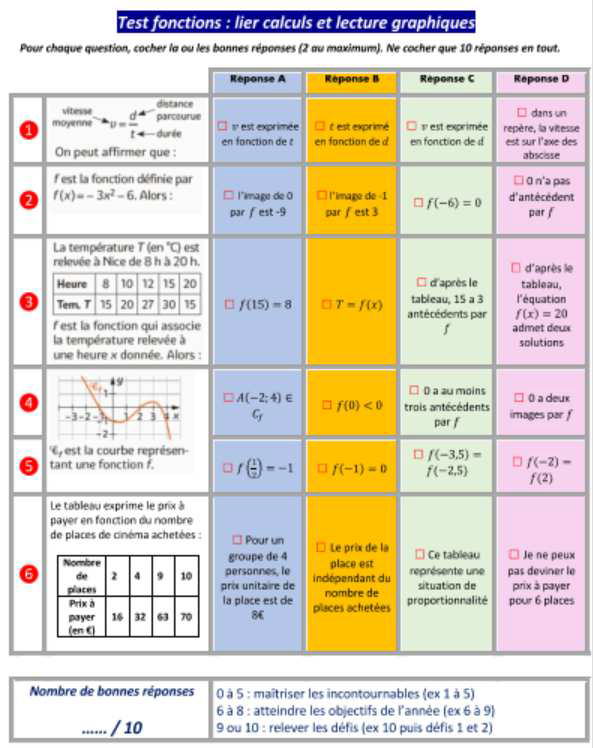
Cette activité permettra de réamorcer les connaissances acquises au cycle 4 mais également d’offrir à chacun la possibilité de se trouver en situation de réussite en début de séance, facilitant alors l’engagement de l’élève dans les tâches proposées : contextes variés (cadres graphique et algébrique), situations issues de la vie courante, évaluation bienveillante, parcours proposé à l’issue adapté aux compétences acquises. Ce questionnaire est vidéoprojetée et les réponses sont visualisées instantanément à l’aide du système Plickers (scan des réponses à l’aide de la caméra d’une tablette ou d’un smartphone pour une obtention instantanée des réponses et d’outils statistiques sur celles-ci). Cela permet alors d’engager un second temps de travail consistant à reprendre chacune des questions avec les élèves en demandant de lire la question, d’expliciter oralement la démarche : que me demande-t-on ? À quelles connaissances fait-on appel ? Quel(s) outils ai-je à disposition ?

En outre, l’oral trouve toute sa place à travers ces rituels. Les réponses fournies mènent à un débat, à des échanges constructifs, structurés et argumentés. Il convient alors de justifier ses choix et de confronter ses propres jugements avec ceux des autres pour analyser, argumenter, formuler et apprendre à utiliser un langage adéquat, compétences visées par les référentiels de mathématiques mais des autres disciplines également (formation du citoyen). Ce diagnostic trouvera son prolongement à travers un parcours diversifié proposé aux élèves, en fonction du score obtenu afin de permettre une progression adaptée à chacun. Son intérêt et son exploitation dans le cadre de ce mémoire sont explicités au paragraphe 4.3.c).

       

C.            Expérimentations et remédiation sur le travail écrit 

           

1.             Développement des écrits dits « intermédiaires »

Les bilans de nombreuses études pointent communément la forte restriction de l’activité écrite des élèves à des écrits de référence (cours, correction des exercices entre autres) menant à un formalisme certes nécessaire mais pouvant inhiber toute démarche individuelle. Ils doivent donc s’accompagner d’écrits de recherche, composante primordiale de déterminante de l’activité mathématique. Ils contribuent à développer chez les élèves des capacités de recherche, de justification des choix, d’argumentation et permettent de créer les conditions de véritables interactions conflictuelles, notamment à travers le travail de groupe : « [...] faire des maths, c’est les FAIRE, au sens propre du terme, les construire, les fabriquer, les produire, que ce soit dans l’histoire de la pensée humaine ou dans l’apprentissage individuel. Il ne s’agit pas, bien sûr, de faire réinventer par les élèves des mathématiques qui existent déjà mais de les engager dans un processus de production mathématique où leur activité ait le même sens que celle des mathématiciens qui ont effectivement forgé des concepts mathématiques nouveaux. Ce qui est important pour l’élève, ce n’est pas de connaître la solution, c’est d’être capable de la trouver luimême et de se construire ainsi, à travers son activité mathématique, une image de soi positive, valorisante, face aux mathématiques » (R. Bkouche, B. Charlot, N. Rouche dans Faire des mathématiques : le plaisir du sens, éditions Armand Collin, 1991). À cet égard, l’importance de la trace écrite lors des phases individuelles de recherche doit constituer un axe de réflexion didactique essentiel chez l’enseignant dans le choix des supports et activités. Se restreindre à des écrits de référence omet cette phase transitoire fondamentale dans le processus d’apprentissage de l’élève lui permettant de prendre part à celui-ci en confrontant sa pensée au lieu de se laisser convaincre. Toutefois, pour en garantir les bienfaits, il faut veiller à assurer une atmosphère bienveillante, autoriser l’élève à essayer, à se tromper, à recommencer, parfois sans aboutir …

2.             Un besoin d’apports théoriques :

Selon les travaux de Jean Julo (Représentation des problèmes et réussite en mathématiques, Presse Universitaire de Rennes, 1995), définit comme suit : « Se représenter un problème, c’est non seulement se représenter un objet particulier défini par un ensemble d’informations qui nous est fourni, mais aussi se représenter la tâche particulière qui est associée à cet objet ». Notons que le travail préliminaire sur l’analyse des consignes évoqué au début de ce mémoire y trouve alors tout son intérêt.

• Principe de construction de la représentation selon J. Julo :

            

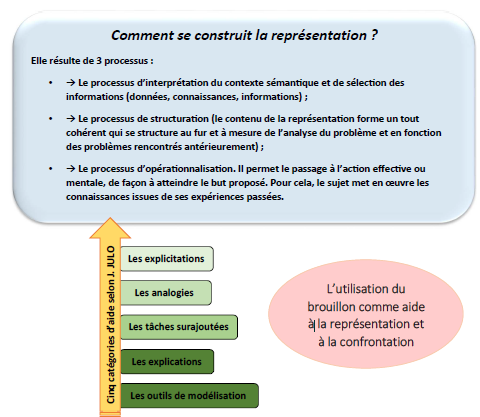
Les écrits intermédiaires (ou de recherche) constituent une aide à l’explicitation du problème, première phase du processus de représentation. Le passage à l’écrit favorise la visualisation des données et des liens qui les unissent. Dans ce cadre, le brouillon est plus qu’un écrit de recherche, c’est aussi l’écrit sur lequel l’élève se représente l’énoncé, permettant ainsi de sortir les informations du texte et de les disposer de manière à les rendre accessibles. Cette action a pour effet de soulager la mémoire de travail.

C’est grâce à l’analyse de ses propres démarches de résolution que l’élève donne du sens aux situations et construit son savoir mathématique. Il faut l’aider à progresser dans sa représentation du problème ». Cela impose, par conséquent, d’ «  avoir une grande tolérance à l’égard des premières productions, accompagnée d’une grande attention à ce qu’elles cherchent à dire, pour une relance positive ». Plusieurs formes de représentation peuvent parfois être envisagées (figure, tableau, arbre, …) : il est bienvenu de les mettre en valeur, et de laisser l’élève choisir celle qui lui convient, en fonction du problème à résoudre.

3.             Mise en application :

• Une transposition de cette démarche sur des tâches usuelles

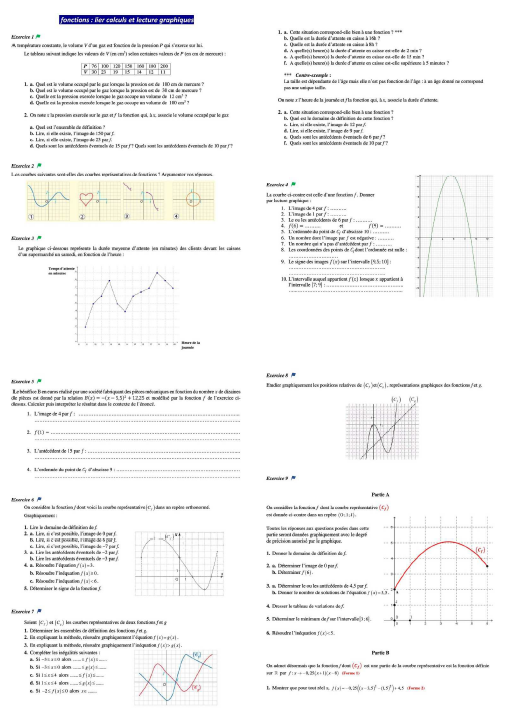
Le parcours diversifié (annexe 9) a servi de support pour la mise en place de ces travaux. Il succédait à l’évaluation diagnostique et était adapté à chaque élève, en fonction du score obtenu. Chacun avait pour mission, à travers son propre parcours et pour chaque exercice, de procéder selon le déroulement suivant :

 1. Surligner le verbe de la question (action à effectuer) ;

 2. Déterminer et écrire à quel(s) point(s) du cours l’exercice fait référence ;

 3. Quel cadre est exploité ? Graphique ? Algébrique ? Les deux ?

 4 . Expliciter une stratégie de résolution ;

 5. Appeler le professeur pour vérification avant de procéder au traitement de l’exercice ;

 6. Rédiger une solution à l’exercice ;

 7. Appeler le professeur pour vérification.

Cette différenciation des exercices a surpris les élèves, notamment laissant apparaître pour certains l’appréhension de ne pas avoir à traiter toutes les notions qui seront évaluées. Il convient donc de les rassurer et de préciser que le noyau commun suffira à être opérationnel pour l’évaluation. Cette mise en confiance s’est révélée nécessaire pour la mise en action de quelquesuns. Le fait que chaque parcours propose initialement un exercice d’entrée très abordable a conforté les élèves les moins à l’aise et a facilité leur activité mathématique. De plus, le traitement des points 1 à 4 ci-dessus s’est avéré rassurant et les observations effectuées lors du premier appel ont témoigné d’une réflexion personnelle souvent aboutie. Le choix d’exercices dits classiques (en lien direct avec les connaissances vues récemment dans le cours) est volontaire pour justifier que la démarche proposée est transposable aux tâches les plus communes et basiques de l’activité mathématique, toujours dans le but de créer des conditions de bienveillance et de stimulation à l’égard des élèves.

           

Celle-ci permet à l’élève d’aborder une activité mathématique engageant l’ensemble des compétences du référentiel. Elle se décline en trois niveaux d’appréhension : débat et conjecture, démonstration, projection à un niveau n+1 (classe de première) à l’aide d’outils TICE afin de faire prendre conscience de la progressivité des apprentissages, de la pertinence des outils mathématiques abordés à chaque niveau, de leur plus-value par rapport au niveau n-1 et de leurs limites lors de tâches plus complexes relevant des niveaux supérieurs. Cela induit une analyse critique de l’élève sur le travail mené et la nécessité de mener une démarche mathématique conforme à celle présentée ci-dessus (points 1 à 7). 

De plus, cette activité pourra trouver pleinement sa place dans une action de formation en prolongement de ce mémoire, celle-ci permettant d’engager toutes les compétences pédagogiques et didactiques entrevues dans ce mémoire. Autour de celle-ci seront dégagés les axes de travail possibles autour de la communication orale et écrite.

Phase 1 : présentation de la tâche et débat sur l’affirmation du présentateur (oral de communication)

  Phase 2 :  mise en place d’une démarche de résolution (selon points 1à 7 )

• Travail écrit de type brouillon avant le second appel
• Travail écrit de type référence avec rédaction d’une solution ;

                                    Entrée réussie de tous les élèves dans l’activité car de niveau cycle 4

Phase 3 : mise en commun et visualisation des solutions proposées puis validation (oral de communication, écrits de référence)

Phase 4 : enrichissement de l’activité pour un traitement en application du chapitre sur le second degré (programme de seconde)

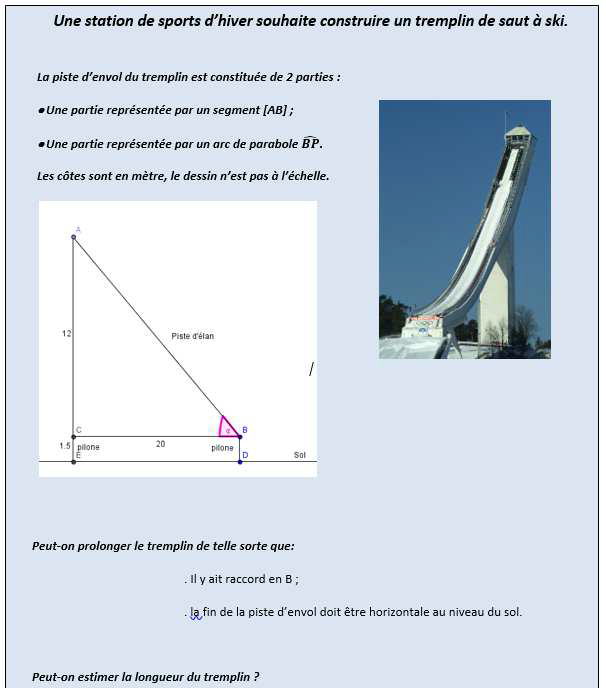
• Travail à l’aide d’outils TICE : conjecture et projection vers la première

                                            (communication numérique)

• Compte-rendu oral sur explicitation de la démarche engagée

                          (oral de communication)

Phase 5 : prolongement vers le niveau n+1

• Débat sur les problèmes sous-jacents ne pouvant être résolus à ce niveau

                          (oral de communication)

• Choix des outils TICE pertinents et résolution à l’aide de ceux-ci : conjecture et projection vers la première (oral de communication et communication numérique)
• Compte-rendu oral sur explicitation de la démarche engagée (oral de communication et communication numérique)

                       

D.            Un travail de synthèse en groupe (séance d’1h30) mêlant oral et écrits de communication

 

Le groupe travaille sur un exercice proche de ceux du parcours, les élèves étant répartis en quatre groupes de besoins homogènes de 3 élèves. Chaque groupe a en charge un exercice différent. Tous les exercices sont des exercices dont le niveau de prise d’autonomie et de difficulté technique sont modulés grâce au parcours adapté.

Tâche demandée :

• Ramassage d’une solution écrite par groupe. Un soin particulier sera apporté à la rédaction → note sur 10 points.
• Pour chaque groupe, présentation orale de la solution proposée (tirage au sort d’un élève dans le groupe) → note sur 10 points.

La grille d’évaluation orale (annexe 10) est donnée aux élèves avant le début du travail, ainsi que des consignes écrites précises : ce sont eux qui évalueront l’élève présentant l’exercice.

           

Consignes concernant la présentation orale :

• Celle-ci ne devra pas dépasser 10 minutes. Pour la grande majorité des exercices, ce temps est suffisant pour présenter la solution. Au-delà de 10 minutes, le professeur interrompt l’élève.
• Pendant la présentation orale d’un élève, les autres élèves doivent prendre la correction dans leurs cahiers/classeurs. Si un point n’est pas clair, ils sont invités à demander des éclaircissements à l’élève au tableau (en veillant à ne pas interrompre le présentateur dans un raisonnement).

Le retour aux élèves : 

Comparaison des notes mises par chacun d’entre eux, repérage des points de convergence et de divergence.

Bilan :

• Exercice effectué sérieusement par les élèves. Le fait de noter donne un cadre plus formel renforçant l’efficacité de l’entraînement à la présentation orale au tableau d’un exercice (entraînement pour la future épreuve du bac).
• Les élèves sont rendus attentifs à l’importance de s’exprimer avec clarté et précision, à avoir une présentation bien organisée au tableau.
• Notation rapide avec la grille (grille du professeur remise aux élèves après passage, permettant ainsi d’avoir une trace écrite de leur performance avec des remarques/commentaires personnels et de voir immédiatement là où ils doivent progresser).
• Relativement aux compétences Expliquer, Argumenter, Communiquer :

• Les phases de mise en commun, d’explication des démarches et des résultats, d’échange d’arguments à propos de leur validité, se sont déroulées oralement favorisant alors le maintien d’un équilibre entre les formulations spontanées utilisées par les élèves et la volonté de mettre en place un langage plus élaboré.

• Les phases de reformulation et de synthèse sont davantage l’occasion de mettre en place un vocabulaire et une syntaxe corrects.

Pour compléter ce travail sur les écrits de communication, tous les élèves ont été invités à réaliser, à la fin du traitement du chapitre sur les fonctions, une carte mentale sur cette notion (l’élaboration d’un tel support ayant été approchée auparavant dans d’autres disciplines).

De plus sont désormais organisés périodiquement des débats sur des sujets de la vie courante, ou sur la véracité (ou non) d’articles de journaux, de propos de reportages TV (un classique : https://youtu.be/Ni4RRDFMwXQ ₎ , …, mêlant mathématiques, esprit critique et discussion, et servant d’activités préparatoires.

IV.           PROJECTION VERS UN ACTE DE FORMATION

 

Il apparaît clairement que les référentiels en vigueur accordent une place conséquente à la compétence liée à la communication. Or forcé de constater que ni les élèves, ni les enseignants de mathématiques dans leur grande majorité ne sont formés à inclure cette dimension dans leur enseignement. Le besoin de formation semble donc évident pour pouvoir y parvenir sereinement et créer les conditions favorables à son acquisition par les élèves.  

Parmi les idées consensuelles sur l’enseignement des mathématiques se trouve la relation de cette discipline à la réalité et le développement de la communication interpersonnelle, compétence de nature interdisciplinaire, visant l’apprentissage avec compréhension. Le rôle de la communication interpersonnelle dans le processus d’enseignement-apprentissage des mathématiques est largement débattu mais les ressources trouvées demeurent moindres dans un contexte incluant particulièrement les mathématiques. La formation envisagée pourrait s’orienter selon ce thème et les tâches mathématiques qui gravitent autour. À mon sens, la valorisation de la relation entre les mathématiques et la réalité des élèves n’est pas assez présente, notamment au lycée. Un discours fréquent des professeurs est : « Les élèves veulent du concret, et quand on leur en propose en exercice ou en devoir, ils sont perdus ». Les mathématiques dites « modernes » ont cherché à resserrer le lien entre les mathématiques enseignées en classe et les mathématiques des mathématiciens, au détriment de la relation avec la réalité. Cette relation ne peut cependant être ignorée car elle permet aux élèves d’attribuer un sens à ce qu’ils apprennent : ils partent de situations concrètes vers des objets et des relations mathématiques abstraites. Dans cette perspective, le rôle de la communication du professeur et des élèves est radicalement différent puisque l’enseignant se doit d’être plus à l’écoute des élèves afin d’inclure leur discours dans un tout cohérent, visant l’apprentissage. Une évolution de ses pratiques intégrant ces facteurs est donc à reconsidérer et à construire. La formation envisageable pourrait alors s’intituler : « La communication : un instrument d’enseignement et d’apprentissage des mathématiques ».

• Références envisagées au référentiel du formateur (annexe 11) :

Voici ci-après (page suivante) un premier état d’une formation envisageable. Bien sûr, la proposition formulée ci-dessus reste hypothétique et soumise à une éventuelle commande institutionnelle mais n’empêche pas de se projeter et d’établir une proposition de cadre à celle-ci. Voici donc une première réflexion quant à une entrée possible (voir propositions en rouge) respectant le référentiel de formation. Ne figurent ci-dessous que les suggestions sous-jacentes à la compétence 1 car il me semble trop long et hors cadre de ce mémoire d’en préciser les contenus et les prolongements. Toutefois, ceux-ci ont déjà été réfléchis et pourraient être explicités ultérieurement si besoin.

 

Quelles que soient les stratégies didactiques et pédagogiques retenues par l’enseignant, dont les choix lui incombent et dont aucun modèle ne peut prévaloir, il ressort clairement que la communication est toujours un élément important de nos pratiques professionnelles. L’enseignant se doit de développer des compétences communicatives interpersonnelles qui vont lui permettre de, bien sûr, transmettre clairement des informations et d’en vérifier leur perception par les élèves tout en créant, chez ceux-ci, de la disponibilité à la réception de cette information grâce à un regain d’intérêt, d’attention et de motivation. Les conditions d’écoute sont optimisées. Cependant, on observe souvent, dans ce contexte particulier, une relation de type symétrique où l’élève s’ajuste aux initiatives de l’enseignant, seul responsable de l’échange en classe. Il convient aussi de préparer l’élève à écouter les autres et à interagir efficacement… 

V.             BILAN, PERSPECTIVES ET CONCLUSION

Il apparaît clairement, les recherches sur le sujet en attestent depuis fort longtemps, que la communication, écrite comme orale, doit apparaître comme tâche de fond dans les apprentissages, aussi et tout particulièrement en mathématiques. Elle apparaît même comme une condition nécessaire à la réussite des élèves. L’enseignement des mathématiques, basé sur la promotion de la communication interpersonnelle entre l'enseignant et les élèves, d’une part, et entre les élèves, d’autre part, favorise l'apprentissage mathématiques avec compréhension.  Comme évoqué au début de ce mémoire, deux facteurs essentiels m’ont guidé vers ce choix de thématique : un constat quotidien d’une communication très descendante entre le professeur et l’apprenant, notamment au lycée aboutissant à cette image de discipline « bête noire des élèves ». Une appréhension certaine à parler de mathématiques est palpable (non choix des mathématiques pour les TPE par exemple). Toutefois, il est à souligner l’importance accordée à la discipline comme outil de compréhension et de développement de la société, observée encore très récemment à travers les intentions de choix des élèves relativement aux futures spécialités de première. La forme envisagée du nouveau baccalauréat a déjà fait émergé ce besoin de formation des élèves mais aussi des enseignants quant aux enjeux et à l’usage d’une communication structurée et interpersonnelle dans les apprentissages. L’accompagnement personnalisé sous sa nouvelle forme, une heure hebdomadaire consacrée à l’oralité et une heure disciplinaire (mathématiques et français) permettent de s’y préparer. Personnellement, ce second créneau m’a servi de support de réflexion et d’expérimentation sur le sujet. Trois phases ont été opérées : 

• Un temps d’observation, d’analyse et de réflexion (pratique et théorique) ayant pour objectif de repérer, de définir et de réunir les conditions favorables à la communication en mathématiques : il s’avère primordial de préparer l’élève à écouter les autres et à interagir efficacement. Un climat de confiance mutuelle associé à la mise en œuvre de stratégies communicatives adaptées aux besoins de l’élève doit également faire partie des objectifs principaux de l'enseignant. Cette instauration d’une écoute active implique de réunir toutes les conditions nécessaires à l’acquisition des compétences visées. Par itérations successives, les élèves vont construire la compréhension par la négociation de sens et, ainsi, apprendre les mathématiques. Dans cette perspective, l’enseignant est obligé d’adapter ses stratégies communicatives afin de générer un climat de confiance tout au long de l’apprentissage et de développer une attitude positive dans sa classe. Développer et assurer des conditions optimales de communication en classe apparaît ainsi clairement comme un outil pédagogique essentiel dans le processus d’enseignement-apprentissage. Prendre le temps d'établir une communication interpersonnelle efficace favorise le respect, la motivation, l'empathie, la prise de décision et le sentiment de progrès. Il s’agit d’un moyen de lutte efficace contre le décrochage scolaire et l’échec grâce au développement de compétences transversales.

• Un deuxième temps d’évaluations diagnostiques visant à établir un parcours différencié, condition nécessaire pour favoriser l’estime de soi chez l’élève et obtenir ainsi son implication. L’échec en résolution de problèmes est souvent dû à des compétences linguistiques fragiles. Les obstacles mathématiques doivent eux-aussi faire l’objet d’une étude. Même en développant des compétences linguistiques et mathématiques, les élèves pêchent souvent par manque de confiance. Il est primordial de se mettre à la place de l’élève afin de comprendre les difficultés qu’il peut rencontrer. Le blocage en mathématiques est bien réel, mais relève, selon moi, d’une décision d’abandon que l’élève est contraint de prendre à un moment de sa scolarité et non à un manque de prédispositions dans la plupart des cas. Enfin, il est essentiel de prendre en compte le niveau de linguistique des élèves afin de construire des apprentissages solides. Il résulte des tests des limitations dans l’expression des idées et du raisonnement mathématique des élèves ainsi que la nécessité, pour le professeur, de repenser l’organisation de son travail en classe autour de tâches d'exploration stimulantes, en connexion avec la réalité, en assurant des moments de communication orale et écrite, de questionnement des élèves et surtout la promotion de la discussion en classe.

• Une phase d’expérimentation de l’oral et des écrits de communication :

Ce jeu de compétences polyvalentes (communiquer-coopérer) se développe alors pleinement. N’oublions pas l’objectif commun qui est de faire des mathématiques, c’est-à dire d’acquérir des connaissances disciplinaires avec pour but d’élaborer des solutions à des problèmes. C’est à ce moment que la communication écrite trouve toute sa place et son importance. Trop souvent réduite à des écrits dits de référence, il paraît fondamental de développer la pratique des écrits qualifiés de complémentaires dans ce mémoire avec comme finalité de faire réellement pratiquer les mathématiques, au sens :

• D’articuler raisonnements oraux et écrits pour une restitution (orale ou écrite) du cheminent ;
• De formaliser et parfois de systématiser ce raisonnement jusqu’à parvenir à l’énoncé de la règle générale ;
• D’argumenter face à la classe ;
• D’acquérir de la rigueur dans l’expression.

Un temps conséquent fut consacré à l’appropriation par les élèves du schéma fonctionnel (page 18). Je retiendrai tout particulièrement les difficultés rencontrées par les élèves à fournir des écrits de type brouillon : difficultés à représenter des informations et des idées mathématiques de façon autonome avec un choix personnel des outils et de la stratégie engagée. Les temps d’échanges oraux avec les élèves ont permis d’atténuer cette relation binaire avec la discipline (je sais ou je ne sais pas). Ces actes oraux et écrits ont permis aux élèves de favoriser l'apprentissage des mathématiques et, en même temps, de développer la capacité à communiquer en mathématiques. La compétence de communication des élèves a besoin de beaucoup de temps pour se développer et se construire. Je tiens également à souligner le temps consacré à la communication écrite car il ne faut pas perdre de vue que l’apprentissage des mathématiques alterne phases d’acquisition des connaissances et phases de restitution ou de réinvestissement. 

Comme il s'agit d'une recherche sur les pratiques des élèves mais aussi implicitement sur celles des enseignants, la réussite semble donc conditionnée à l'expertise de ces derniers. Il en découle alors la proposition de formation citée ci-dessus. Sa forme et ses contenus ont été définis selon mes besoins ressentis au fur et à mesure des expérimentations. Elle n’a aucune valeur de préconisation mais résulte humblement d’impressions personnelles et de pistes permettant de développer et/ou de conforter mes pratiques. 

J’espère que ces quelques pages auront permis au lecteur de percevoir le plaisir que j’ai eu à élaborer ce mémoire et à partager ces expérimentations avec mes élèves et des collègues. Des améliorations ont été démontrées quant à la capacité à communiquer et réfléchir mathématiquement. Cependant, je n’omets pas les conditions propres au dispositif de l’accompagnement personnalisé (une dizaine d’élèves maximum par cycle de cinq semaines). La transposition des pratiques suggérées dans ce mémoire à la classe entière a bien sûr engagé une organisation des espaces et des modalités de fonctionnement (organisation en îlots par exemple pour certaines activités). Un bilan plus objectif et substantiel pourra être dressé en fin d’année mais nul doute que les actions engagées ainsi que les échanges avec les élèves auront été source de stimulation et d’épanouissement, ce mémoire permettant d’avoir la faveur de les partager. 

BIBLIOGRAPHIE

• Revue française de pédagogie n°96, article de Gérard Vergnaud, 1991.
• PISA à la loupe, juin 2016.
• Communication et interactions, Adler et Proctor, 2011.
• Brochure IREM « Langages et apprentissages mathématiques ; utilisation d’outils informatiques »,
• Denis Butlen, Grand N n°79, IREM de Grenoble, 2007.
• Stella Baruk, Echec et Maths, 1973.
• Enseigner l’oral ?, Claudine Garcia-Debanc, Isabelle Delcambre, Repères recherches en didactique du français langue maternelle, 2001.
• L'entretien d'explicitation en situation scolaire, IREM de Lyon, 2003.
• Enseigner les mathématiques, didactique et enjeux de l’apprendre, Jean-Luc Dorier et Ghislaine Gueudet, Belin, 2019.
• Elisabeth Bautier, Lire et écrire pour apprendre, conférence université de Liège, mars 2017.
• Education & didactique N3/Vol.12, Presses Universitaires de Rennes, 2018.
• Pierre Vermersch et Maryse Maurel, Pratiques de l’entretien d’explicitation, 1997.
• Chabanne et Bucheton, Parler et Écrire pour penser, apprendre et se construire, PUF 2002.
• Les traces écrites des élèves en mathématiques, IGEN mathématiques, 2001.
• Alain Lieury, n°130 de la revue Etudes de Linguistique Appliquée, 2003.
• L’oral en mathématiques dans PRATIQUES Math, bulletin n°45 des groupes de recherche Math-collège, Math-lycée et Primaire du CEPEC, 2011.
• Bkouche, B. Charlot, N. Rouche, Faire des mathématiques : le plaisir du sens, éditions Armand Collin, 1991
• Jean Julo, Représentation des problèmes et réussite en mathématiques, Presse Universitaire de Rennes, 1995

SITOGRAPHIE

• Vidéo BFMTV, dailymotion.com/video/x657vlt
• Vidéo France 2, https://youtu.be/Ni4RRDFMwXQ
• INFO, https://www.cairn.info/revue-le-francais-aujourd-hui-2011-3-page-107.htm
• Portail des IREM, http://www.univ-irem.fr/spip.php?rubrique231
• EDUSCOL programmes, https://www.education.gouv.fr/pid285/bulletin_officiel.html?pid_bo=38502 PERSÉE, www.persee.fr
• IFÉ Institut Français de l’Éducation, ife.ens-lyon.fr
• Vidéo conférence Sylvie Cèbe, http://centre-alain-savary.ens-lyon.fr/CAS/education-prioritaire/ressources/theme-1perspectives-pedagogiques-et-educatives/realiser-un-enseignement-plus-explicite/enseigner-explicitement-pour-quoi-quiquand-quoi-comment

 

ANNEXES

Annexe 1

Annexe 2

 

Annexe 3

 

Annexe 4

 

Annexe 5

 

Annexe 6

 

Annexe 7

 

Annexe 8

 

Annexe 9

 

Annexe 10

 

Annexe 11